Main Research
Online Prediction for Partially Observed Stochastic System
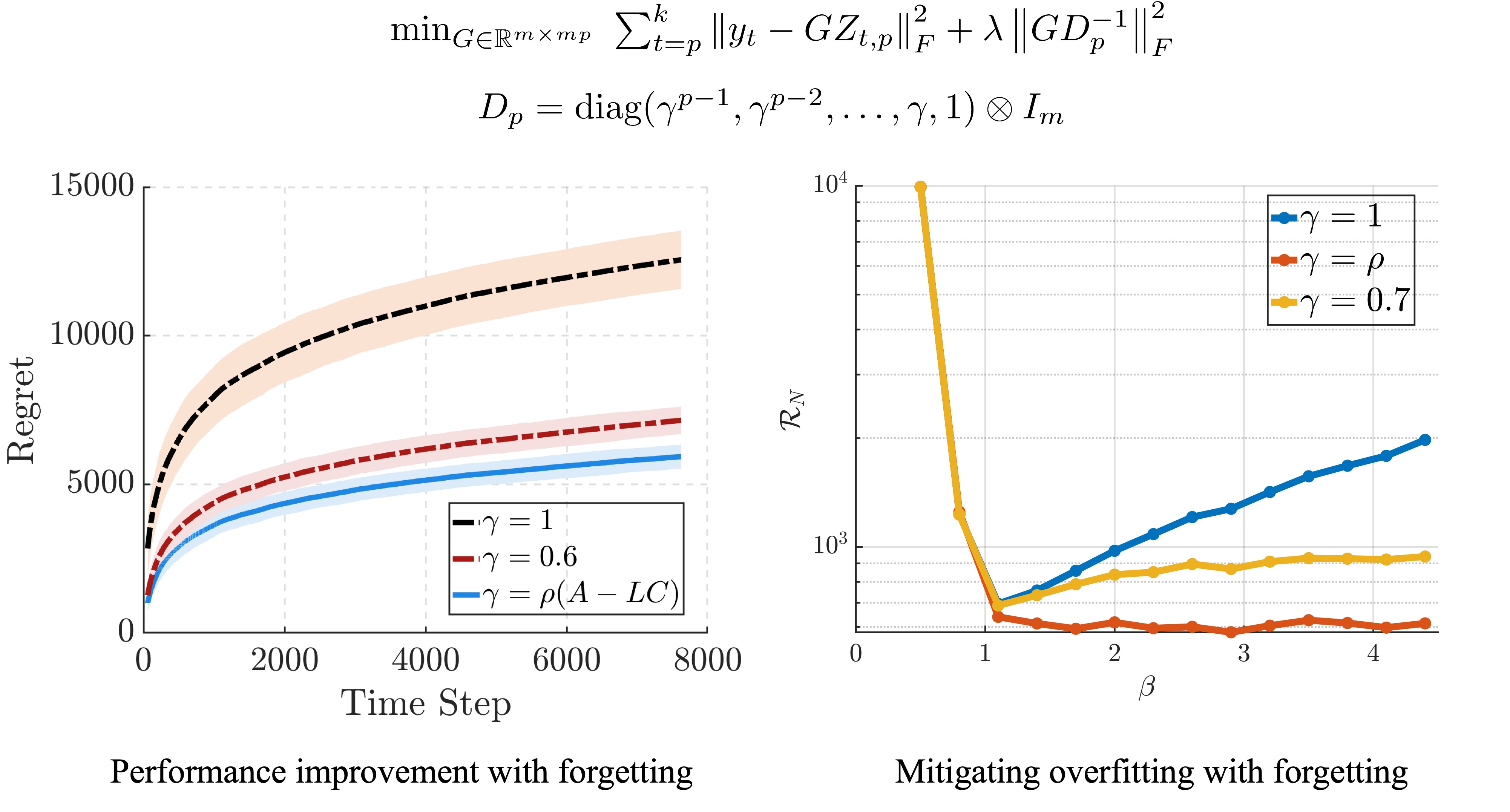
The problem of sequential online prediction of dynamical systems from data is fundamental across many fields and has a long-standing history. Its applications span from control systems, robotics, natural language processing, and computer vision. For a linear stochastic system, we can leverage the Kalman filter to predict the future system states and observations by properly filtering the past observations. In many applications, however, obtaining explicit models and reliable noise characterizations is impractical, especially when input-output relationships are complex to identify. This has motivated growing interest in learning prediction policies directly from data, without full knowledge of the underlying system. From model-based prediction to data-driven approaches, a central challenge is how to parameterize the prediction policy. Instead of identifying an explicit model from data, some recent studies focus on learning a prediction policy directly from input-output data. These methods exploit the Kalman filter’s structure and parameterize the prediction policy as a linear function of past inputs and outputs, estimating the weights via online learning. A very interesting result is that, by leveraging past outputs for future prediction, if the amount of collected data is large enough and the backward horizon is sufficiently long, then the online least squares-based predictor can approach the optimal model-based Kalman predictor as closely as possible.
In this work, we notice that the imbalanced nature of the prediction model can easily lead to overfitting and thus degrade prediction accuracy. Therefore, we tackle this problem by injecting an inductive bias into the regression model via exponential forgetting to rebalance the regression model properly, then utilize the online least squares-based method to learn this balanced model. Unlike conventional discounting or forgetting methods, which primarily reweight the online data stream, our forgetting approach directly adjusts the regression model parameters. Moreover, by properly choosing the forgetting factor $\gamma$, our algorithm will guarantee a logarithmic regret with respect to the optimal Kalman filter. While utilizing the forgetting factor may not reduce the order of the logarithmic regret bound, it can effectively reduce the constant in the regret bound. Finally, we demonstrate that the proposed algorithm effectively reduces overfitting by ensuring the regret scales logarithmically with the length of the backward horizon. In contrast, in the absence of forgetting, the regret grows linearly with the backward horizon length.
Harmonic-Coupled Riccati Equations and its Applications in Distributed Filtering
The distributed filtering problem is about estimating the state of a large-scale dynamical system with spatially distributed sensor networks. The communication among sensor nodes in the network is restricted, which means that at each time step, each node can only get access to partial observation information. One of the common problems in distributed filtering is the lack of mathematical tools to reveal the steady-state performance of filtering algorithms with weak local observability.
In this work, we managed to formulate a novel kind of matrix equations called harmonic-coupled Riccati equations (HCRE), which contains multiple Riccati-like matrix equations with solutions coupled using harmonic means. We first manage to discover conditions for the existence and uniqueness of solutions to HCRE, then find an iterative law with low computational complexity to obtain the unique group of solutions. Based on this newly established mathematical tool, we further formulate the closed-form expression of the steady-state estimation error covariance of the consensus-on-information-based distributed filtering (CIDF) algorithm into the solution to a discrete-time Lyapunov equation (DLE). This leads to a significant reduction in the conservativeness of traditional performance evaluation techniques for CIDF. The obtained results are remarkable since they not only enrich the theory of coupled Riccati equations but also provide a novel insight into the synthesis and analysis of distributed filtering algorithms.

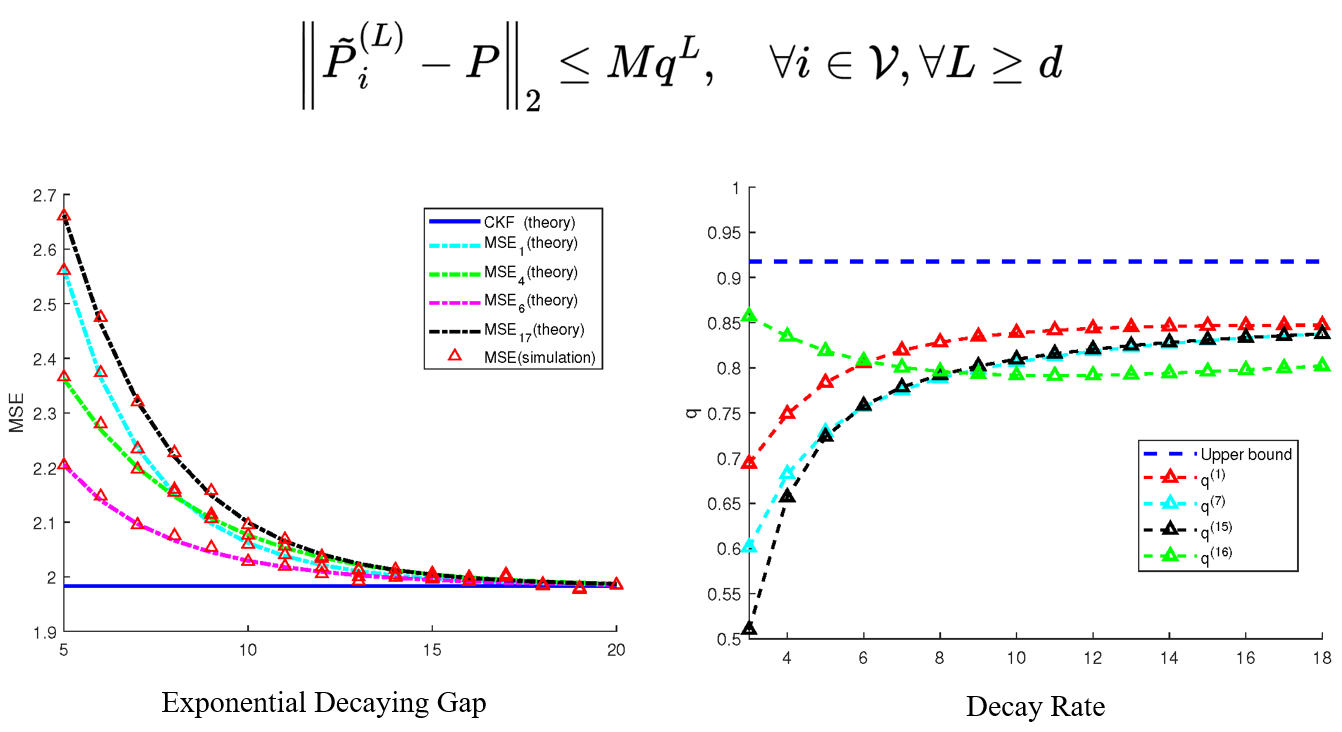
Optimality Analysis: Bridging the Centralized Kalman Filtering and Consensus-based Distributed Filtering
For consensus-based distributed filtering, one standard view is that through infinite consensus fusion operations during each sampling interval, each node in the sensor network can achieve optimal filtering performance with centralized filtering. However, due to the limited communication resources in physical systems, the number of fusion steps cannot be infinite. Due to the lack of sufficient mathematical tools, the literature is unable to clearly describe the effect of a finite fusion step on the performance of the distributed filtering algorithm, especially on the gap between distributed and centralized filtering.
In this work, we concentrate on the optimality analysis of consensus-based filtering, especially the performance degradation analysis of the consensus-on-measurement-based filtering (CMDF) algorithm with finite consensus fusion operations. First, by introducing a modified discrete-time algebraic Riccati equation and several novel techniques, we demonstrate that the convergence of the estimation error covariance matrix with the increase of time step is guaranteed under a collective observability condition. In particular, the steady-state covariance matrix can be simplified as the solution to a discrete-time Lyapunov equation. Moreover, we manage to formulate the performance degradation induced by reduced fusion frequency in the infinite series form, which establishes an analytical gap between the performance of the CMDF with finite fusion steps and that of centralized filtering. Meanwhile, this gap also provides a trade-off between filtering performance and communication cost. We further demonstrate that the steady-state estimation error covariance matrix exponentially converges to the centralized optimal steady-state performance as the fusion operations tend to infinity during each sampling interval, and the convergence speed is not slower than the norm of the second-largest eigenvalue of the adjacency matrix corresponding to the communication topology.